Step 1: Please create your three ticker tapes. When you get them, please write on the tape WHAT you did to get that type of tape. Mark position 0 and tape to the whiteboard under the clock.
Step 2: Ticker walk: Take a strip that you believe has constant motion and one that has non-constant motion. Get a whiteboard and divide it in half. For the first strip, create a sample graph of total distance vs. time, and a sample graph for interval distance vs. time on the bottom half. In both cases, time is the independent variable. NOTE: I said sketches, which means you do not have to measure the distance from dot to dot exactly. Just estimate.
Step 3: On a second whiteboard, write a CLAIM regarding your second strip. The strip itself is EVIDENCE, but you may also want to use a graph or a table. Here, you must represent the motion of at least half of the entire strip. Explain your REASONING for your claim.
Second 20 minutes: Reading, class discussion and mathematical models of straight lines
Last half of class--Motion Man Activity
This activity is done in groups of 2 or 3. If there are more than three names on a sheet, it WILL NOT be accepted.
Click on the activity above. It will eventually launch a new Java script in a separate window. If you are having trouble, we can help. DO NOT click on the icon repeatedly or you will open up multiple copies of the program.
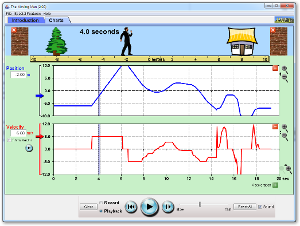
Print the Moving Man Activity for your group. This will be handed in, along with your packet at the end of the class period today. Moving Man Activity
====================================DO not start this until directed-=====================
NOTES and PROCESSING For the following situations, sketch a d-t, v-t, and non-zero a-t graphs that show up in your notes (this activity is modified from here). When you get done with the graphs, send me a picture for your group
A) A man moving from the left of the screen (-8 m) to the house (8m) at a constant 2 m/s (adjust the v-slider).
B) A man moving from 0 to the house at a faster pace than above. C) A man standing still at 4 m.
D) A man moving from 0 to the house at a fast pace then moving back to 0 at a slower pace (slide the man manually).
E) A man moving from 16 m to the tree m at a fast pace of (3 m/s).
F) A man moving from 0 to the house, speeding up as he walks (an acceleration of 1 m/s/s).
G) The man stands still while he talks on his cell phone at the middle of the sidewalk, then walks toward the house at a constant rate trying to get better cell reception. He comes to a sudden stop when the coverage is good (about a meter before the house) and stands still to finish his conversation.
H) The man starts close to the tree, stands still for a little while, then walks toward the house at a constant rate for a while, then slows gradually to a stop.
I) A man wakes up from his nap under the tree and speeds up toward the house. He stops because he is worried that he dropped his keys. He stands still as he searches his pockets for his keys. Once he finds them, he continues calmly to walk toward the house and then slows to a stop as he nears the door.
Click on the activity above. It will eventually launch a new Java script in a separate window. If you are having trouble, we can help. DO NOT click on the icon repeatedly or you will open up multiple copies of the program.
Print the Moving Man Activity for your group. This will be handed in, along with your packet at the end of the class period today. Moving Man Activity
====================================DO not start this until directed-=====================
NOTES and PROCESSING For the following situations, sketch a d-t, v-t, and non-zero a-t graphs that show up in your notes (this activity is modified from here). When you get done with the graphs, send me a picture for your group
A) A man moving from the left of the screen (-8 m) to the house (8m) at a constant 2 m/s (adjust the v-slider).
B) A man moving from 0 to the house at a faster pace than above. C) A man standing still at 4 m.
D) A man moving from 0 to the house at a fast pace then moving back to 0 at a slower pace (slide the man manually).
E) A man moving from 16 m to the tree m at a fast pace of (3 m/s).
F) A man moving from 0 to the house, speeding up as he walks (an acceleration of 1 m/s/s).
G) The man stands still while he talks on his cell phone at the middle of the sidewalk, then walks toward the house at a constant rate trying to get better cell reception. He comes to a sudden stop when the coverage is good (about a meter before the house) and stands still to finish his conversation.
H) The man starts close to the tree, stands still for a little while, then walks toward the house at a constant rate for a while, then slows gradually to a stop.
I) A man wakes up from his nap under the tree and speeds up toward the house. He stops because he is worried that he dropped his keys. He stands still as he searches his pockets for his keys. Once he finds them, he continues calmly to walk toward the house and then slows to a stop as he nears the door.
No comments:
Post a Comment